Boolean Algebra
Boolean Algebra is a set of rules, laws and theorems by which logical operation can be expressed mathematically. It is convenient and systematic way of expressing and analyzing the operation of digital circuits and systems.
Example: F= x+y’z
Fig: logic diagram
Logic Operation
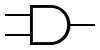
| NAND |  |
 |
|
||||||||||||||||||
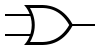
| NOR |  |
 |
|
||||||||||||||||||
| XOR | 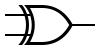 |
 |
|
||||||||||||||||||
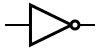
| XNOR | 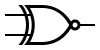 |
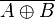 or or  |
|
||||||||||||||||||
Source: Wikipedia
Purpose of Boolean Algebra
1. Express in algebraic form a truth table relationship between binary variables
2. Express in algebraic form the i/o relationship of logic diagram
3. Find simpler circuits for the same function
Basic Identities of Boolean Algebra
- x+0 = x
- x.0 = 0
- x+1 = 1
- x.1 = x
- x+x = x
- x.x = x
- x+x’ = 1
- x.x’ = 0
- (x’)’ = x
Laws:
- Commutative Law:
(A+B) = (B+A)
(A.B) = (B.A)
2. Associative Law:
A+(B+C) = (A+B)+C
A.(B.C) = (A.B).C
3. Distributive Law:
A.(B+C) = A.B+A.C
4. Involution Law:
__
__
A = A
5. Idempotent Law:
x+x+x+x+x+x+x+x…… = x
x.x.x.x.x.x.x.x.x.x.x…… = x
When all the input of an OR gate or an AND gate are shorted to get a one input one output gate, the logic gate of the input is same as the logic state of the output.
6. Absorption Law:
A.(A+B) = 1
LHS: A.A+A.B Distributive Law
= A+A.B Idempotent Law
= A(1+B) Distributive Law
= A.1
=A
Dual of a boolean expression
Replace (+) by (.) or vice versa and complementing 0’s and 1’s.
Example:
A.B = A+B
A.B+A.B = (A+B).(A+B)